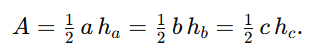Dreieck Rechner
Mit unserem dreiecksrechner können Sie jedes beliebige Dreieck berechnen online und Winkel, Seitenlängen sowie Fläche in Sekundenschnelle ermitteln. Geben Sie einfach die bekannten Werte ein – der dreieck online berechnen-Assistent liefert Ihnen sofort alle fehlenden Größen.
Dreiecksrechner - Beliebiges Dreieck
Seiten
Winkel
Zusätzliche Werte
Ergebnisse:
Verwendete Berechnungsmethode:
Hinweise zur Berechnung:
- SSS (3 Seiten): Verwendung des Kosinussatzes zur Berechnung der Winkel
- SWS (2 Seiten, 1 eingeschlossener Winkel): Kosinussatz für fehlende Seite
- SSW (2 Seiten, 1 nicht eingeschlossener Winkel): Sinussatz
- WSW/WWS (2 Winkel, 1 Seite): Winkelsummensatz + Sinussatz
- WWW (3 Winkel): Keine eindeutige Lösung für Seitenlängen
Geben Sie genau drei Werte ein, um das Dreieck zu berechnen. Die Summe der Winkel muss 180° betragen.
Funktionsweise des Dreieck-Rechners
Der dreieck berechnen-Rechner bietet verschiedene Rechenwege wie SSS (drei Seiten bekannt), SAS (zwei Seiten und eingeschlossener Winkel) oder ASA (zwei Winkel und eingeschlossene Seite).
Nach Auswahl der Methode und Eingabe Ihrer Werte (z. B. Seitenlängen oder Winkel) berechnet der winkel berechnung dreieck online automatisch die fehlenden Seiten, Winkel, den Umfang, die Fläche sowie die Höhen auf jeder Seite.
Beispiel anhand Ihrer Eingaben
In Ihrem Beispiel wurden alle drei Seiten angegeben: a = 10 cm, b = 6 cm und c = 6 cm.
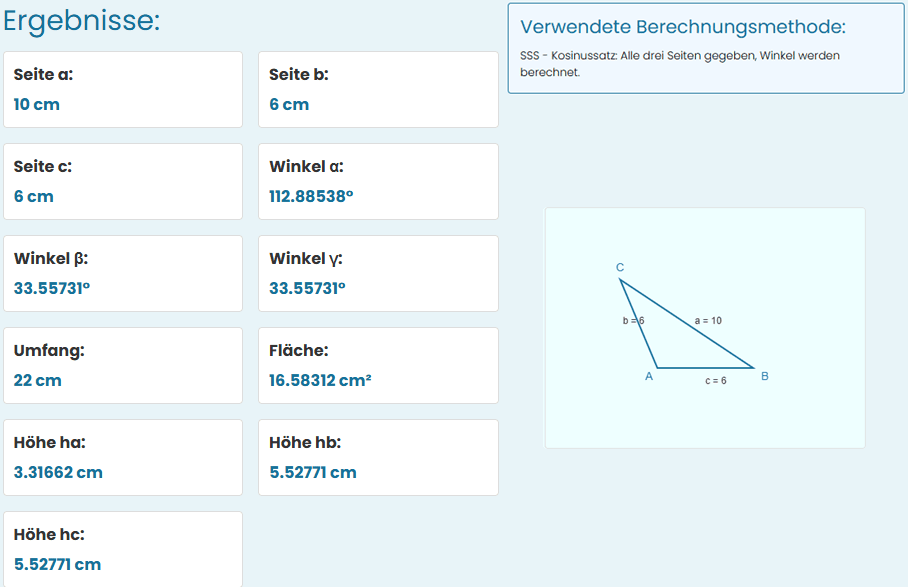
Der dreiecks rechner wählte die SSS-Methode und ermittelte mithilfe des Kosinussatzes den Winkel α als etwa 112,89 °, wobei die beiden anderen Winkel β und γ je 33,56 ° betragen. Anschließend berechnete der dreieck winkel rechner den Umfang zu 22 cm und die Fläche zu etwa 16,58 cm². Über die Flächenformel ergaben sich die Höhen: hₐ ≈ 3,32 cm, h_b ≈ 5,53 cm und h_c ≈ 5,53 cm.
Berechnung fehlender Seiten und Winkel
Fall SSS
Sind alle drei Seiten a, b, c bekannt, berechnet man die Winkel über den Kosinussatz in folgender Form:
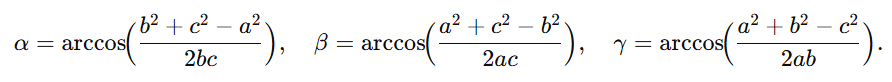
Fall SWS
Liegt ein Winkel zwischen zwei bekannten Seiten, z. B. α zwischen b und c, so nutzt man den Kosinussatz zur Berechnung der dritten Seite und zieht anschließend die Wurzel:
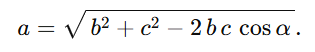
Analog erhält man b oder c, wenn man β oder γ einsetzt.
Fall SSW
Zwei Seiten und ein nicht eingeschlossener Winkel erfordern den Sinussatz
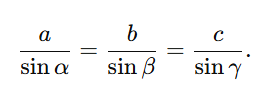
Möchte man zum Beispiel b ermitteln und kennt a, α und β, so gilt
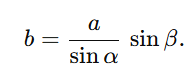
Umgekehrt lassen sich Winkel wie β durch
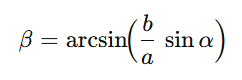
bestimmen. Auf die mögliche Zweideutigkeit (ambiguous case) ist zu achten.
Fall WSW bzw. WWS
Zunächst ergänzt man den dritten Winkel über den Winkelsummensatz
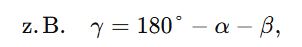
und wendet dann den Sinussatz an, um die fehlenden Seiten zu berechnen.
Fall WWW
Drei gegebene Winkel legen nur die Form fest, nicht die Größe. Es existieren unendlich viele zueinander ähnliche Dreiecke.
Umfang, Höhen und Flächeninhalt
Der Umfang beträgt u=a+b+cu = a + b + cu=a+b+c. Die Höhe auf Seite a berechnet sich direkt als
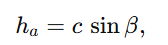
und entsprechend hb=asinγ, hc=b sinαh_c = b\,\sin αhc=bsinα. Sind nur die Seiten bekannt, führt man zunächst
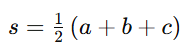
ein und erhält
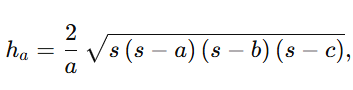
bzw. analog für hbh_bhb und hch_chc. Der Flächeninhalt ergibt sich dann aus A=12 a ha=12 b hb=12 c hc.